Why Prompt Caching Doesn't Solve Your Latency Problems
If you’ve been working with LLMs recently, you’ve encountered prompt caching. Basically, every major LLM provider offers it, including OpenAI, Anthropic, and Gemini.
Prompt caching works like this: you give the model the same prompt prefix as the one in the cache, and you get something like a 10x cost reduction in input tokens and a reduction in time-to-first-token (TTFT).
For example, if I’m running a simple Q&A bot that helps people learn about Reinforcement Learning: An Introduction, I can cache the entire book. That way, when people ask me questions about it, I can spend 10x less per input token and give them faster responses.1
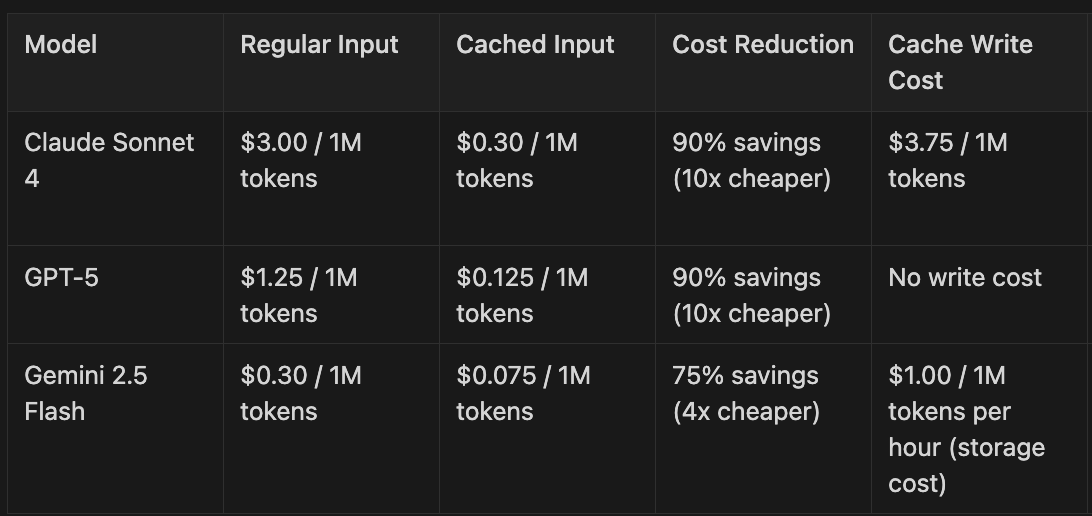
The cost savings are clear from the table, but what about latency? When I first began using prompt caching, I thought it would solve all my latency problems. I had originally been thinking about prompt caching in the context of a chat application, and there, time-to-first-token (TTFT) matters quite a bit for the user experience.
Typically, TTFT increases as a function of the number of input tokens. I had thought that caching would allow me to feed in as many input tokens as I liked without any increase in latency. That turned out to be wrong, and it wasn’t clear to me why, so I investigated. This is a write-up of that investigation. We’ll touch on how prompt caching works below the API boundary and why the size of your cache still matters for TTFT.
Background recap
At the heart of transformers is the attention mechanism.2
Typically, the formula is written like this:
Q denotes a matrix during training and can be either a matrix (batch inference) or a vector (single query) during inference. In this case, Q is the query matrix for the last token, meaning that Q has dimensions 1 × dk.
However, both K and V are matrices that grow with the sequence length. For example, if we’ve already decoded five tokens, K and V both contain five rows. This is because when we compute the attention scores for the most recent token, we want to take all past tokens into account.
For example, if we have a prompt like “What is the capital of France?” which tokenizes into [”What”, “is”, “the”, “capital”, “of”, “France”, “?”] and we’ve begun decoding, we’ll have the following:
Q: 1 × dk — a query vector representing “?” our last token
K: 7 × dk — a key matrix with key vectors for each of our seven tokens
V: 7 × dk — a value matrix with value vectors for each of our seven tokens
Suppose we decode, and “Paris” is our eighth token. Then at the next step, we’ll have
Q: 1 × dk — a query vector representing “Paris,” our last token
K: 8 × dk — a key matrix with key vectors for each of our eight tokens
V: 8 × dk — a value matrix with value vectors for each of our eight tokens
Crucially, the first seven rows of K and V in this decoding step for “Paris” are identical to the K and V matrices from when we decoded “?”.
This insight is what enables caching. When we compute K and V at step n, we save them. Then, when we begin decoding at step n+1 rather than calculating the entire K and V matrices, we can compute row n+1 for K and V and append it to the K and V cache from step n.
This is all that prompt caching is, from what I can tell. Aptly, it is also called KV-caching.3
Why the KV-cache size matters for TTFT
You might think that if you have a KV-cache for the first 1,000 tokens, then decoding the 1,001st token will take just as long as decoding a single token from an empty prompt.
This isn’t quite right. First, loading the KV-cache into memory depends on the GPU’s high bandwidth memory (HBM), which means that larger KV caches (which are a function of how long the sequence is) will still lead to higher TTFT.
And even if you have the KV-cache loaded, TTFT will still be higher for the 1,001st token than for the 1st token. Operations like QKᵀ are linear in the sequence length because performing this matmul means we take the dot product of vector Q with every row of K.
The Experiment
Maybe all of this theory doesn’t matter in practice. I checked by running an experiment. Here’s the setup.
Experiment setup:
Model: Qwen2.5-14B
Attention implementation: FlashAttention-2 (swapped in — Qwen2.5-14B defaults to GQA).
Precision: float16.
Batch size: 1.
GPU: A100-80GB
Warmup: 2 iterations, then 10 repeats averaged (we run the first decode twice to initialize the GPU, then run 10 trials and average over them)
The linear trend we see here is consistent with the theoretical cost of computing QKᵀ above. But, more practically, what this trend tells us is that on average, I pay ~4.69 ms of TTFT for every 10k tokens I add to my context.4
So, while KV-caching reduces cost, TTFT still grows with every token in context. You will have to resort to other tricks if you have a massive number of tokens in context and strict TTFT constraints.
Thanks to Chris Hua for reading a draft of this.
This is not out of the goodness of their hearts. Providers save over 90% of GPU FLOPs using prompt caching for longer prompts.
For the purposes of this post, I'll be focusing on traditional attention, which is almost certainly not what these model providers have implemented. They're more likely to be using newer methods like Multi-Head Latent Attention or Grouped Multi-Query Attention.
To be more precise, prompt caching is an API-level concept and KV-caching is a specific technique, but I assume that the way that API providers are implementing prompt caching is primarily with KV-caching.
This only applies to Qwen2.5-14B. The slope depends on kernel and attention variant (e.g., FlashAttention-2, GQA, sliding windows), but the linear trend is universal for dense, non-local attention.



